by Andy Jiang | Aug 16, 2017 | Math
Cool Divisibility Rules
Special Thanks to: Patrick Burnett
You would probably learn the divisibility rules for 2, 3, 4, 5, 6, 8, and 9 in school. But what about the divisibility rule for 7? Well, the divisibility rule for 7 is quite simple, and quite interesting. All you have to do is take off the last digit of the number, multiply it by 2, and subtract that from the rest of the number. Here’s an example: Say you want to know if 469 is divisible by 7. If 469 is divisible by 7, then 46 – 2×9 must also be divisible by 7, and 46 – 18 = 28. Since 28 is divisible by 7, 469 is divisible by 7. That’s a quick way to check divisibility without having to do long division. Here’s another example: You want to know if 999999 is divisible by 7. If 999999 is divisible by 7, then 99999 – 2×9 = 99981 must be divisible by 7, and if 99981 is divisible by 7, then 9998 – 2×1 = 9996 must be divisible by 7, and if 9996 is divisible by 7, then 999 – 2×6 = 987 must be divisible by 7, and if 987 is divisible by 7, 98 – 2×7 = 84 must be divisible by 7, and we know that 84 is divisible by 7. Therefore, 999999 is divisible by 7.
This trick can be generalized to different numbers. For the mathematical minded: If you want to prove if a number 10X + Y is divisible by P, where X is a positive integer, and Y is an integer from 0 to 9 inclusive, and find a K such that 10K + 1 is divisible by P, then X – KY must also be divisible by P.
In layman’s terms: You know that the divisibility rule for 7 involves subtracting 2 times the last digit from the other digits. A similar trick can be applied to other odd numbers. The reason why the last digit is multiplied by 2 is because 21 is the least multiple of 7 that ends in a 1. The divisibility rule for 13 is similar, but you would have to subtract 9 times the second digit from the other digits, as 91 is the least multiple of 13 ending in a 1, and for 17, you would multiply the last digit by 5, as 51 is the least multiple of 17 ending in a 1.
Are you suspicious? I don’t blame you, but see for yourself. Multiply 17 by a large number on a calculator, and try the trick on the large number. For example, you can try 83521. 8352 – 5×1 = 8347, 834 – 5×7 = 799, 79 – 9×5 = 34, and 34 is divisible by 17, so 83521 must also be divisible by 17.
You can do this with any odd ending in 1, 3, 7, or 9, as all odds ending in these numbers will eventually have a multiple ending in 1. Try to find the divisibility rule for 97. Scroll down to see the answer when you find it.
Answer: Subtract 29 times the second digit from the first.
by Andy Jiang | Aug 1, 2017 | Math
The Cool Thing about Repeating Decimals
Get out your calculator and type in 331/999 and press enter. What do you get? Something along the lines of 0.331331331…? Now type in 21/9999 and press enter. What do you get? 0.002100210021…? This cool trick works with any fraction less than 1 with all nines in the denominator, which are always of the form 10A – 1, for some number A. Here’s a proof:
- Say x = 0.A1A2A3…An…… (Where x is a repeating decimal, and A1A2A3…An is the string of numbers that is repeated in the decimal, and n is the length of the string)
- If we multiply both sides by 10n, then we would get: x10n = A1A2A3…An.A1A2A3…An…, because the decimal point is moved n times to the right
- x10n = A1A2A3…An.A1A2A3…An… is the same thing as A1A2A3…An + 0.A1A2A3…An, and since 0.A1A2A3…An = x, then x10n = A1A2A3…An + x
- By subtracting both sides of the equation by x, you would get x10n – x = A1A2A3…An, or x(10n – 1) = A1A2A3…An
- By dividing both sides by 10n – 1, you would get… x = (A1A2A3…An)/(10n – 1)
- Therefore, by substituting 0.A1A2A3…An… for x, you would get…
- A1A2A3…An… = (A1A2A3…An)/(10n – 1), where A1A2A3…An is a string of numbers of length n, and 10n – 1 is a string of n 9s, for example 103 – 1 = 1000 – 1 = 999
This proof is a generalization of a trick you learn in middle school. Say you want to convert 0.21… into a fraction. You would set that equal to x to get x = 0.21… and multiply both sides by 100 to get 100x = 21.21…, which is 100x = 21 + 0.21…, or 100x = 21 + x. Next you would subtract x from both sides to get 99x = 21, and x = 21/99. Don’t forget to simplify J.
Note: If you want to do something like 7/99999, add 0s in front of the 7 to make the numerator and denominator have the same number of digits to get 00007/99999, and the decimal of that would be .000070000700007…
by Andy Jiang | May 10, 2017 | Math
You may be discouraged from joining the math team because you don’t think you’re not good at it, but like many other things in life, you can get better at math by working hard at it and with the proper attitude. All you need is a love of math, the desire to make yourself better, and a winning attitude. If you don’t like math, then maybe joining math team can change your opinion on math. At math competitions, you commonly get problems that require you to think outside the box and think of creative solutions, unlike traditional high school math. If you are interested or just want to try it out, talk to your school’s math team coach and ask him or her about joining the team. He or she would be more than willing to help you out. If your school doesn’t have a team and you want to start one, take initiative and find a teacher who is willing to sponsor and coach a math team. There are lots of math competitions in Georgia every year, where you get a chance at showing off your math skills, finding opportunities to improve, and simply having fun. If you see a problem you don’t understand, don’t feel discouraged. If you are willing to learn the tricks, you will get better and better at it, and eventually, if you do consistently well at math competitions, you can make it on one of Georgia’s state ARML teams, where the best are selected from all over Georgia to compete in a competition involving teams from all over the US and even from other countries, like Colombia and China. You get to interact with kids who love math just like you from all over Georgia and stay at a dorm at the University of Georgia to #DoMaTh and/or socialize with the kids and compete for a chance for fun and international glory.
by Andy Jiang | Apr 18, 2017 | Math
Why I Don’t Like Mathematical Induction
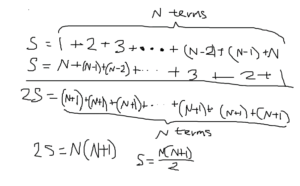
Everybody has opinions, and you can even have opinions about math. I, for one, don’t particularly like the method of mathematical induction. Why? Because it doesn’t completely tell you “why”. For example, you can use mathematical induction to prove that 1 + 2 + 3 + 4 + … + n = n(n+1)/2. Great, we know that the formula works, but where does the formula come from? A much more elegant method to prove that formula is derivation. There are many ways to derive that formula, and one method is by writing 1 + 2 + 3 + 4 + … + n forwards and backwards and by adding them together twice. That way, you can see how twice the sum would be n(n+1) (see the visual), so the sum would be n(n+1)/2. By deriving the formula, you see why the formula is the way it is, and you’ll be able to connect the formula to the nature of the series. Also, mathematical induction is not a method to make equations, as it can only be used if the equation is given. With induction, you may prove old equations, but with derivation, you’ll be able to make new equations.
by Andy Jiang | Mar 28, 2017 | Math
Cool Thing About Pythagorean Triplets
There is a cool property of all odd numbers except one, they can all form Pythagorean triplets. A Pythagorean triplet is any set of positive integers a, b, and c that satisfy the equation a2 + b2 = c2. For example, a= 3, b= 4, and c= 5 is a Pythagorean triplet because 32 + 42 = 52. If a is any odd number except 1, it can make a Pythagorean Triplet of the form a= a, b= (a2 – 1)/2, and c= (a2 – 1)/2 + 1, or b + 1. You can prove this by substituting b and c with b= (a2 – 1)/2 and c= (a2 – 1)/2 + 1 in the equation a2 + b2 = c2. “a” cannot be even for this case because if a were even, (a2 -1)/2 would not be a whole number, and a cannot be one, because then, b would be zero. For all other odd numbers, this would work, and Pythagorean Triplets of this form include…
a= 5, b= 12, c= 13
a= 7, b= 24, c= 25
a= 9, b= 40, c= 41

